문자열 패턴 매칭
패턴 매칭에 사용되는 알고리즘
- 고지식한 패턴 검색 알고리즘(Brute Force)
- 라빈-카프 알고리즘
- 보이어-무어 알고리즘
- KMP 알고리즘
고지식한 알고리즘(Brute Force)
본문 문자열을 처음부터 끝까지 차례대로 순회하면서 패턴 내의 문자들을 일일이 비교하는 방식으로 동작
$O(NM)$
p[] : 찾을 패턴, t[] : 전체 텍스트
M : 찾을 패턴의 길이, N : 전체 텍스트의 길이
BruteForce(p[], t[])
i <- 0, j <- 0
WHILE j< M AND i < N
IF t[i] != p[j] // 실패
i <- i-j
i <- -1
i <- i + 1
j <- j + 1
IF j == M : RETURN i - M
ELSE : RETURN i
고지식한 패턴 매칭 알고리즘의 시간 복잡도
- 최악의 경우 시간 복잡도는 텍스트의 모든 위치에서 패턴을 비교해야 하므로 $O(MN)$이 됨
- 비교횟수를 줄일 수 있는 방법은 없는가?
라빈-카프 알고리즘
- 문자열 검색을 위해 해시 값 함수를 이용
- 패턴 내의 문자들을 일일이 비교하는 대신에 패턴의 해시 값과 본문 안에 있는 하위 문자열의 해시 값만을 비교
- 최악의 시간 복잡도는 $O(MN)$이지만 평균적으로는 선형에 가까운 빠른 속도를 가지는 알고리즘
숫자로 이루어진 문자열에서, “4321”을 찾자
패턴의 해시 값을 계산한다.
- 각 자리의 숫자에 자리값을 곱하여 더한다.
- 해시값은 “4321”이라는 문자열이 아니라 정수값 4321이 된다.
찾고자 하는 문자열에서 4자리씩 해시값을 계산한다.
- 찾고자하는 문자열에서 한글자씩 이동하여 패턴 길이만큼 읽어서 해시 값을 계산하는 것이 아니라, 새로 추가되는 문자와 그 전에 읽었던 값을 이용하여 해시값을 구한다. (sliding window : SlidingWindowTest. java)
- 여기서는 전 값에서 맨 앞자리 수 를 빼고 10을 곱한 후 새로운 수를 더해준다.
고려사항
- 처음 해시 값을 구할 때는 찾고자 하는 문자열에서 패턴 길이 만큼 읽어서 구한다.
- 길이가 커지면 길이를 일정 자리수로 맞추기 위해 mod 연산을 취한다.
- 따라서 해시 값이 일치하더라도 실제 패턴이 일치하지 않을 수 있기 때문에 해시 값이 일치하면 문자열 일치를 검사해야한다.(이를 해시 충돌이라 한다.)
보이어 무어 알고리즘
- 오른쪽에서 왼쪽으로 비교
- 보이어-무어 알고리즘은 패턴에 오른쪽 끝에 문자가 불일치하고 이 문자가 패턴 내에 존재하지 않는 경우, 이동거리는 무려 패턴의 길이 만큼이 된다.
- 최악의 시간복잡도는 $O(MN)$이지만 최선의 시간 복잡도는 $O(N/M)$이며 평균적으로는 가장 빠른 속도를 가진 알고리즘이다.
- 오른쪽 끝에 있는 문자가 불일치 하지만 이 문자가 패턴 내에 존재할 경우, 패턴에 일치하는 문자를 찾아서 한꺼번에 이동한다.
skip 배열 만들기
- skip[ch] : 본문 ch 문자에서 패턴 불일치가 발생했을 때 본문포인터의 skip 횟수
- 패턴에 포함되지 않는 문자들은 본문 포인터가 패턴 길이 만큼 skip해야 하므로 패턴의 길이가 skip배열의 값이 됨.
- 패턴 문자들의 skip 배열값(패턴 마지막 문자는 제외한다.)
- (패턴 문자열의 길이 - 1) : 각 패턴 문자의 인덱스
KMP 알고리즘
- Knuth-Morris-Pratt Algorithm
- 불일치가 발생한 텍스트 문자열의 앞 부분에 어떤 문자가 있는지를 미리 알고있으므로, 불일치가 발생한 앞 부분에 대하여 다시 비교하지 않고 매칭을 수행
- ex) S = “aaaaaaaaab”, W=”aaaab”가 있는데 S와 W에 a가 계속 반복되므로 S의 매 위치마다 최소 5번의 비교를 하게 된다.
- 패턴을 전처리하여 부분일치 테이블 배열 pi[k]을 구해서 잘못된 시작을 최소화함
- pi[k] : 처음부터 k인덱스까지를 끝으로 하는 부분 문자열에서 일치하는 접두사와 접미사가 일치하는 최대 길이
- 시간 복잡도 : $O(M+N)$
-
패턴을 이용하여 부분일치 테이블 배열 작성
→ 매칭이 실패했을 때 패턴 포인터가 돌아갈 곳을 계산
-
패턴의 0번째 인덱스를 제외한 각 인덱스마다 맨 앞부터 해당 인덱스까지의 부분문자열 중 접두사와 접미사가 일치하는 최대 길이로 계산하여 작성
- 맨 앞부터 해당 인덱스까지의 길이가 2이상인 부분문자열 중 접두사이면서 접미사인 최대 문자열
- “ababaca”의 부분일치 테이블은 “ababaca”와 비교해가며 얻는다.
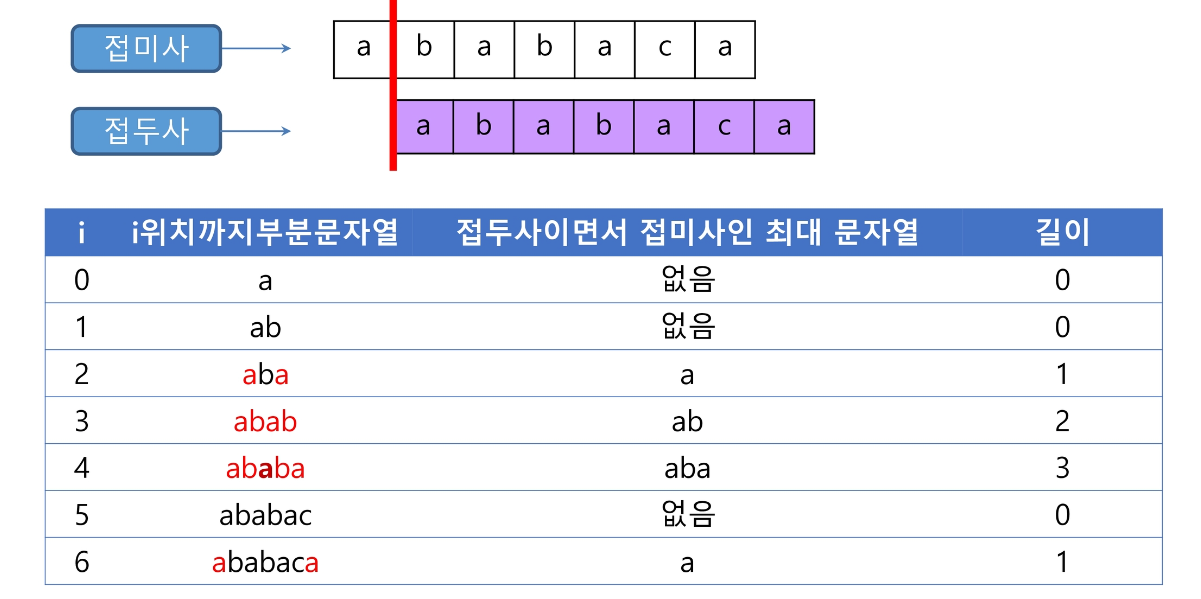
- 부분일치 테이블을 사용해서 일치하는 패턴을 찾는다.