탐욕 기법
탐욕(Greedy) 알고리즘
- 탐욕 알고리즘은 최적해를 구하는 데 사용되는 근시안적인 방법
- 최적화문제(optimization)란 가능한 해들 중에서 가장 좋은(최대 또는 최소) 해를 찾는 문제이다.
- 일반적으로, 머리 속에 떠오르는 생각을 검증 없이 바로 구현하면 Greedy 접근이 된다.
- 여러 경우 중 하나를 선택 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다.
- 각 선택 시점에서 이루어지는 결정은 지역적으로 최적이지만, 그 선택들을 계속 수집하여 최종적인 해답을 만들었다고 하여, 그것이 최적이라는 보장은 없다. (검증 요구)
- 일단, 한번 선택된 것은 번복하지 않는다. 이런 특석 때문에 대부분의 탐욕 알고리즘들은 단순하며, 또한 제한적인 문제들에 적용된다.
탐욕 기법 - 배낭 짐싸기
knapsack 문제의 전형적 정의
- S : 물건들의 집합
- W_i : item_i의 무게, P_i = item_i의 값
- W : 배낭이 수용 가능한 총 무게
- 문제 정의
$\sum_{item_i \in A} w_i <= W$를 만족하면서 $\sum_{item_i \in A} P_i$가 최대가 되도록
$A \subseteq S$가 되는 $A$를 결정하는 문제
knapsack 문제 유형
- 0-1 knapsack
- 배낭에 물건을 통째로 담아야 하는 문제
- 물건을 쪼갤 수 없는 경우
- Fractional Knapsack
- 물건을 부분적으로 담는 것이 허용되는 문제
- 물건을 쪼갤 수 있는 경우
0-1 knapsack에 대한 완전 검색 방법
- 완전 검색으로 물건들의 집합 S에 대한 모든 부분집합을 구한다.
- 부분집합의 총 무게가 W를 초과하는 집합을 버리고 나머지 집합에서 총 값이 가장 큰 집합을 선택할 수 있다.
- 물건의 개수가 증가하면 시간 복잡도가 지수적으로 증가한다.
- 크기 n인 부분집합의 수 2^n
탐욕 기법 활용 - 회의실 배정
- 시작시간과 종료시간( $s_i$, $f_i$ )이 있는 n개의 활동들의 집합 $A = {A_1, A_2, …, A_n}$, $1<= i <=n$에서 서로 겹치지 않는(non-overlapping) 최대개수의 활동들의 집합 $S$를 구하는 문제
- 양립 가능한 활동들의 크기가 최대가 되는 $S_{0,n+1}$의 부분집합을 선택하는 문제
- 종료시간 순으로 활동들을 정렬한다.
- $S_{0,n+1}$는 $a_0$의 종료시간부터 $a_{n+1}$의 시작시간 사이에 포함된 활동들
활동 선택 문제(Activity-selection problem)
탐욕 기법의 적용
$S_{i,j}$를 풀기 위해
- $a_i$ 종료 시간부터 시작 가능한 활동 중 종료 시간이 가장 빠른 $a_m$ 선택
- $S_{i,j} = {a_m} \cup S_{m,j}$의 해집합
$S_{i,j}$는 $a_i$의 종료 시간부터 $a_j$의 시작시간 사이에 포함된 활동들
탐욕 기법을 적용한 반복 알고리즘
MeetingRoomTest.java
A : 활동들의 집합, S : 선택된 활동(회의)들 집합
s_i : i활동의 시작시간, f_i : i활동의 종료시간, 1<=i<=n
Sort A by finish time
S <- {A_1}
j <- 1 // 선택된 활동 집합 중 마지막 활동
FOR i in 2 -> n
IF f_j <= s_i
S <- S U {A_i}
j <- i
- 종료 시간이 빠른 순서로 활동들을 정렬한다.
- 첫번째 활동(A_1)을 선택한다.
- 선택한 활동(A_1)의 종료시간보다 빠른 시작 시간을 가지는 활동은 무시(skip)하며 같거나 늦은 시작시간을 갖는 활동을 선택한다.
- 선택된 활동의 종료시간을 기준으로 뒤에 남은 활동들에 대해 앞의 과정을 반복한다.
탐욕 알고리즘의 필수 요소
탐욕적 선택 속성(greedy choice property)
- 탐욕적 선택은 최적해로 갈 수 있음을 보여라. -> 즉, 탐욕적 선택은 항상 안전하다.
최적 부분 구조(optimal substructure property)
- 최적화 문제를 정형화하라 -> 하나의 선택을 하면 풀어야 할 하나의 하위 문제가 남는다.
[원문제의 최적해 = 탐욕적 선택 + 하위 문제의 최적해] 임을 증명하라.
탐욕 알고리즘의 예
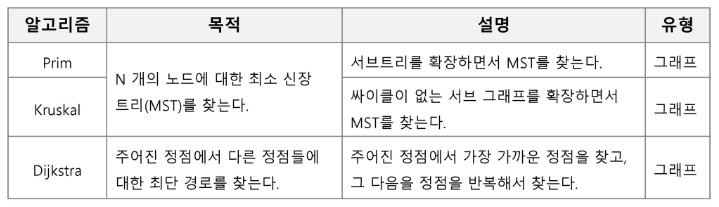
대표적인 탐욕 기법의 알고리즘들
탐욕 기법 응용 - 동전 자판기
Ex_동전자판기_Test.java
동전을 많이 사용하는 법 구하기
보유한 동전의 총 금액을 구하고 지불해야할 금액을 뺀 나머지의 값을 구한다
그 나머지 값을 최소한의 동전을 사용하여 지불 할 수 있는 방법을 구한다.